59. Spiral Matrix II (螺旋矩阵 II)

题目链接： 59. Spiral Matrix II

Difficulty: Medium

Topics: Array, Matrix, Simulation

Question

Given a positive integer $n$, generate an $n \times n$ $matrix$ filled with elements from $1$ to $n^2$ in spiral order.

Example 1:

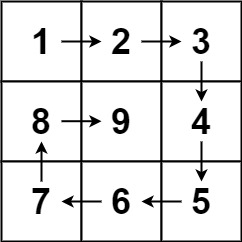
Input: n = 3
Output: [
  [1, 2, 3],
  [8, 9, 4],
  [7, 6, 5],
]

Example 2:

Input: n = 1
Output: [[1]]

Constraints:

• $1 \le n \le 20$

解题思路

方法1:

思路

这和前面那个题基本一样，唯一区别就是我们需要先初始化一个空数组然后往里面填数据。还是顺时针进行循环，每个位置从1开始顺序填入数据一直到$n\times n$为止。

代码

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        result = [[0 for _ in range(n)] for _ in range(n)]

        # 定义四个边界
        top, right = 0, n - 1
        left, bottom = 0, n - 1

        val = 1
        while val <= n * n:
            # 从左到右遍历上边界
            for col in range(left, right + 1):
                result[top][col] = val
                val += 1
            top += 1  # 上边界收缩

            # 从上到下遍历右边界
            for row in range(top, bottom + 1):
                result[row][right] = val
                val += 1
            right -= 1  # 右边界收缩

            if top <= bottom:
                # 从右到左遍历下边界
                for col in range(right, left - 1, -1):
                    result[bottom][col] = val
                    val += 1
                bottom -= 1  # 下边界收缩

            if left <= right:
                # 从下到上遍历左边界
                for row in range(bottom, top - 1, -1):
                    result[row][left] = val
                    val += 1
                left += 1  # 左边界收缩

        return result

复杂度

• 时间：我们先创建了一个空的矩阵，需要消耗$O(n^2)$。然后循环更新里面的数值，消耗时间也是$O(n^2)$，总计当然也是$O(n^2)$。
• 空间：除了最后返回的result，只设置了4个额外的边界和1个储存当前插入值的$int$，总额外空间消耗只有$O(1)$。