54. Spiral Matrix (螺旋矩阵)

题目链接： 54. Spiral Matrix

Difficulty: Medium

Topics: Array, Matrix, Simulation

Question

Given an $m \times n$ $matrix$, return all elements of the $matrix$ in spiral order.

Example 1:

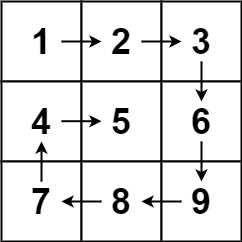
Input: matrix = [
  [1, 2, 3],
  [4, 5, 6],
  [7, 8, 9],
]
Output: [1, 2, 3, 6, 9, 8, 7, 4, 5]

Example 2:

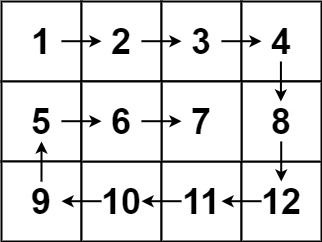
Input: matrix = [
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9, 10, 11, 12],
]
Output: [1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7]

Constraints:

• $m == matrix.length$
• $n == matrix[0].length$
• $1 \le m, n \le 100$
• $-100 \le matrix[i][j] \le 100$

解题思路

方法1:

思路

题目要求是螺旋记录到列表里，实际上我们可以发现就是4个边不断收缩，并且总数没变。那么我们就可以也设置4个边界，并且用同样的方式进行顺时针旋转。每次运行while loop都是在进行一次完整的顺时针循环。

代码

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        m, n = len(matrix), len(matrix[0])
        result = []

        # 定义四个边界
        top = left = 0
        right = n - 1
        bottom = m - 1

        while len(result) < m * n:
            # 从左到右遍历上边界
            for col in range(left, right + 1):
                result.append(matrix[top][col])
            top += 1  # 上边界收缩

            # 从上到下遍历右边界
            for row in range(top, bottom + 1):
                result.append(matrix[row][right])
            right -= 1  # 右边界收缩

            if top <= bottom:
                # 从右到左遍历下边界
                for col in range(right, left - 1, -1):
                    result.append(matrix[bottom][col])
                bottom -= 1  # 下边界收缩

            if left <= right:
                # 从下到上遍历左边界
                for row in range(bottom, top - 1, -1):
                    result.append(matrix[row][left])
                left += 1  # 左边界收缩

        return result

复杂度

• 时间：因为我们对给定的矩阵的每一个元素都进行了遍历，这样消耗的时间就是$O(m \cdot n)$，并没有其他的时间消耗。
• 空间：除了最后返回的result，只设置了4个额外的边界$int$，总额外空间消耗只有$O(1)$。