跳到主要内容

73. Set Matrix Zeroes (矩阵置零)

题目链接： 73. Set Matrix Zeroes

Difficulty: Medium

Topics: Array, Hash Table, Matrix

Question​

Given an m×nm \times n integer matrix matrixmatrix, if an element is 00, set its entire row and column to 00's.

You must do it in place.

Example 1:

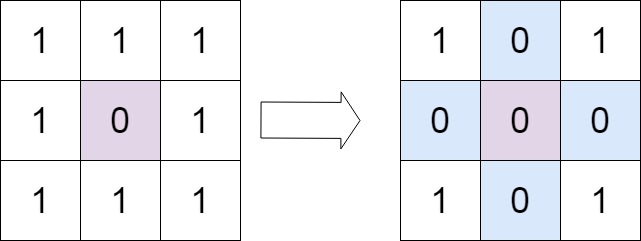
Set Matrix Zeroes - Example 1

Input: matrix = [
  [1, 1, 1],
  [1, 0, 1],
  [1, 1, 1],
]
Output: [
  [1, 0, 1],
  [0, 0, 0],
  [1, 0, 1],
]

Example 2:

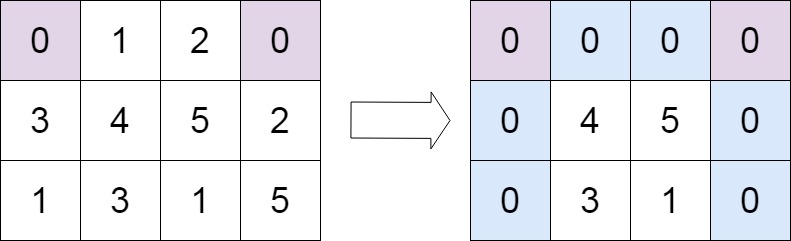
Set Matrix Zeroes - Example 2

Input: matrix = [
  [0, 1, 2, 0],
  [3, 4, 5, 2],
  [1, 3, 1, 5],
]
Output: [
  [0, 0, 0, 0],
  [0, 4, 5, 0],
  [0, 3, 1, 0],
]

Constraints:

  • m==matrix.lengthm == matrix.length
  • n==matrix[0].lengthn == matrix[0].length
  • 1≤m,n≤2001 \le m, n \le 200
  • −231≤matrix[i][j]≤231−1-2^{31} \le matrix[i][j] \le 2^{31} - 1

解题思路​

方法1:​

思路​

我们根据题目要求需要把0所在的行和列全部替换，那么我们就首先遍历整个matrix的每一个元素，把0所在的行和列信息记录下来，然后统一清零。

代码​

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        m = len(matrix)
        n = len(matrix[0])
        position_row = set()
        position_col = set()
        for row in range(m):
            for col in range(n):
                if matrix[row][col] == 0:
                    position_row.add(row)
                    position_col.add(col)

        for row in position_row:
            matrix[row][:] = [0] * n

        for col in position_col:
            for row in range(m):
                matrix[row][col] = 0

复杂度​

  • 时间：因为我们对给定的矩阵的每一个元素都进行了遍历，这样消耗的时间就是O(m⋅n)O(m \cdot n)。然后把记录下来的所有行和列也全都遍历修改好，最差的时间消耗也是O(m⋅n)O(m \cdot n)，总和为O(m⋅n)+O(m⋅n)=O(m⋅n)O(m \cdot n) + O(m \cdot n) = O(m \cdot n)。
  • 空间：因为创建了两个额外的set去储存对应的信息，总额外空间消耗达到了O(m+n)O(m + n)。

方法2:​

思路​

我们考虑如何实现O(1)O(1)空间的算法，这才是我们真正的目标。那么思路就是将数组的第一行和第一列作为我们之前标记所使用的position_rowposition\_row和position_colposition\_col，这样就可以节省掉那O(m+n)O(m+n)的空间。

当然还需要考虑这第一行第一列也有可能出现0，比如第一列中如果出现一个0，会导致第一列全都清零，同时它所在的那行也会被清空。我们会发现这里只需要标记是否需要清空这个第一列就行，那么我们就单独保存两个boolean值就好。

代码​

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        m = len(matrix)
        n = len(matrix[0])

        # 标记第一行和第一列是否需要置零
        first_row_zero = any(matrix[0][col] == 0 for col in range(n))
        first_col_zero = any(matrix[row][0] == 0 for row in range(m))

        # 使用第一行和第一列作为标记
        for row in range(1, m):
            for col in range(1, n):
                if matrix[row][col] == 0:
                    matrix[row][0] = 0
                    matrix[0][col] = 0

        # 根据标记置零
        for row in range(1, m):
            for col in range(1, n):
                if matrix[row][0] == 0 or matrix[0][col] == 0:
                    matrix[row][col] = 0

        # 处理第一行
        if first_row_zero:
            matrix[0][:] = [0] * n

        # 处理第一列
        if first_col_zero:
            for row in range(m):
                matrix[row][0] = 0

复杂度​

  • 时间：yysy这一眼望过去一片for loop，实际上我们可以拆分开来分析
    • 判断第一行和第一列这里消耗了O(m+n)O(m+n)
    • 标记的时候消耗了O((m−1)⋅(n−1))O((m - 1) \cdot (n - 1))
    • 根据标记清零又来了一遍O((m−1)⋅(n−1))O((m - 1) \cdot (n - 1))
    • 处理第一行的时候消耗为O(n)O(n)，第一列为O(m)O(m)，这里加起来就是O(m+n)O(m + n)
    • 总计为O(m⋅n)O(m \cdot n)了。
  • 空间：因为只创建了两个额外的boolean去储存第一列和第一行是否需要清空，总额外空间消耗达就只有O(1)O(1)了。