498. Diagonal Traverse (最大连续 1 的个数)

题目链接： 498. Diagonal Traverse

Difficulty: Medium

Topics: Array, Matrix, Simulation

Question

Given an $m \times n$ matrix $mat$, return an array of all the elements of the array in a diagonal order.

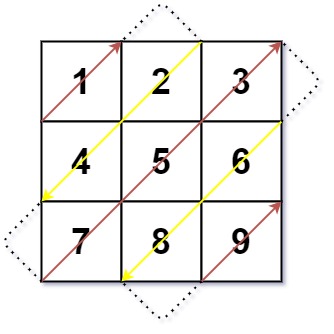
Example 1:

Input: mat = [
  [1, 2, 3],
  [4, 5, 6],
  [7, 8, 9],
]
Output: [1, 2, 4, 7, 5, 3, 6, 8, 9]

Example 2:

Input: mat = [
  [1, 2],
  [3, 4],
]
Output: [1, 2, 3, 4]

Constraints:

• $m == mat.length$
• $n == mat[i].length$
• $1 \le m,n \le 10^4$
• $-10^5 \le matt[i][j] \le 10^5$

解题思路

方法1:

思路

根据题目要求要沿着对角线把元素放到输出的数组里，那么我们就需要知道对角线的遍历方式，以及如何在方向切换时调整遍历的顺序。

1. 对角线的概念：每一条对角线上的元素，它们的索引 $(i, j)$ 之和是相同的，比如：

   • $(0, 0)$ 在第 0 条对角线
   • $(0, 1)$ 和 $(1, 0)$ 在第 1 条对角线
   • $(0, 2)$、$(1, 1)$ 和 $(2, 0)$ 在第 2 条对角线
   • $(2, 1)$ 和 $(1, 2)$ 在第 3 条对角线
   • $(2, 2)$ 在第 4 条对角线
   备注

   可以看到我们上面每条对角线上的元素之和，都与对角线的序数相等。

2. 方向切换：

   • 当 $sum = i + j$ 是偶数时，我们从左下到右上遍历（图中红线）。
   • 当 $sum = i + j$ 是奇数时，我们从右上到左下遍历（图中黄线）。

3. 边界处理：在遍历时需要特别注意矩阵的边界。不同的方向切换时，可能会遇到数组越界问题，需要根据情况调整行和列的索引。

代码

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        if not mat or not mat[0]:
            return []

        m, n = len(mat), len(mat[0])
        result = []
        direction = 1  # 1 表示从左下到右上，-1 表示从右上到左下
        row, col = 0, 0

        for _ in range(m * n): # m * n是总元素个数
            result.append(mat[row][col])
            if direction == 1:
                if col == n - 1: # 右边界
                    row += 1
                    direction = -1
                elif row == 0: # 上边界
                    col += 1
                    direction = -1
                else:
                    row -= 1
                    col += 1
            else:
                if row == m - 1: # 下边界
                    col += 1
                    direction = 1
                elif col == 0: # 左边界
                    row += 1
                    direction = 1
                else:
                    row += 1
                    col -= 1

        return result

复杂度

• 时间：因为我们遍历了举证中的每一个元素，又因为矩阵的大小为$m \times n$，所以我们的总时间复杂度为$O(m \times n)$。
• 空间：不考虑输出结果，我们只额外设置了几个$int$类型的变量，所以总空间复杂度为$O(n)$

方法2:

思路

上面一样的思路，我们还是根据对角线的编号来。这次我们的思路着重关注于对角线上的元素坐标之和为对角线的序号$k$。

• 我们的总对角线条数为$k = m + n - 1$
• 同样的我们根据对角线的序号$k$是偶数（左下到右上）还是奇数（右上到左下）来决定行进方向。
• 还有一个情况就是当$k$超过中线后，对于偶数，每次就都是从底边开始（$m - 1$）了；对于奇数，每次就都是从最右边（$n - 1$）开始了。

代码

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        if not mat or not mat[0]:
            return []

        m, n = len(mat), len(mat[0])
        result = []

        for k in range(m + n - 1):
            # 根据 k 的值，确定方向
            if k % 2 == 0:
                # 从左下到右上
                # k过了最中间的对角线后，每次row就是从最大(m - 1)开始了
                row = min(k, m - 1)
                col = k - row
                while row >= 0 and col < n: # 边界
                    result.append(mat[row][col])
                    row -= 1
                    col += 1
            else:
                # 从右上到左下
                # k过了最中间的对角线后，每次col就是从最大(n - 1)开始了
                col = min(k, n - 1)
                row = k - col
                while col >= 0 and row < m: # 边界
                    result.append(mat[row][col])
                    row += 1
                    col -= 1

        return result

复杂度

• 和前一个一样没有区别。但我个人会觉得这种需要考虑的case更少逻辑更简单。

方法3:

思路

前面两种思路基本都是一样的，就是按照对角线的方向进行元素的添加，控制好方向和边界就好。还有一种思路是直接根据对角线的序号添加到字典中，对于偶数的进行反响输出，奇数正向。

比如按照上图中的例子来说：会被储存在如下

• $diagonals[0] = [1]$
  • 偶数，反转，一个就不用动了。
• $diagonals[1] = [2,4]$
  • 奇数，直接用
• $diagonals[2] = [3,5,7]$
  • 偶数，反转，$[7,5,3]$
• $diagonals[3] = [6,8]$
  • 奇数，直接用
• $diagonals[4] = [9]$
  • 偶数，反转，一个就不用动了。

这样最后结果连起来就是$[1,2,4,7,5,3,6,8,9]$，也就是我们所期望的结果。

代码

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        if not mat or not mat[0]:
            return []

        diagonals = {}
        m = len(mat)
        n = len(mat[0])
        for i in range(m):
            for j in range(n):
                if (i + j) not in diagonals:
                    diagonals[i + j] = [mat[i][j]]
                else:
                    diagonals[i + j].append(mat[i][j])

        result = []
        for k in range(len(diagonals)):
            if k % 2 == 0:
                # 偶数对角线需要反转（从左下到右上）
                result.extend(diagonals[k][::-1])
            else:
                # 奇数对角线保持顺序（从右上到左下）
                result.extend(diagonals[k])

        return result

复杂度

• 时间：因为我们遍历了举证中的每一个元素，又因为矩阵的大小为$m \times n$，所以我们的总时间复杂度为$O(m \times n)$。
• 空间：不考虑输出结果，因为保存了一个字典和原来的矩阵储存的数据量一样，所以总额外的空间复杂度也为$O(m \times n)$。