289. Game of Life (生命游戏)

题目链接： 289. Game of Life

Difficulty: Medium

Topics: Array, Matrix, Simulation

Question

According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."

The board is made up of an $m \times n$ grid of cells, where each cell has an initial state: live (represented by a $1$) or dead (represented by a $0$). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the $m \times n$ grid $board$, return the next state.

Example 1:

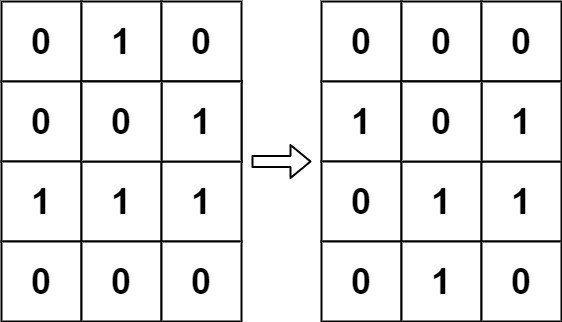
Input: board = [
  [0, 1, 0],
  [0, 0, 1],
  [1, 1, 1],
  [0, 0, 0],
]
Output: [
  [0, 0, 0],
  [1, 0, 1],
  [0, 1, 1],
  [0, 1, 0],
]

Example 2:

Input: board = [
  [1, 1],
  [1, 0],
]
Output: [
  [1, 1],
  [1, 1],
]

Constraints:

• $m == board.length$
• $n == board[i].length$
• $1 \le m, n \le 25$
• $board[i][j]$is$0$or$1$.

Follow up:

• Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
• In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?

解题思路

方法1:

思路

创建一个新的$result$矩阵，在这个矩阵中储存更新后的值（避免直接在board上更新影响下一次循环）。因为我们的规则有8个方向，我们就需要在8个方向分别防止溢出。如果没到边界就对周围存在的1进行计数，最后根据当前细胞本身为0还是1使用不同的规则在result的对应位置进行更新即可。

代码

class Solution:
    def gameOfLife(self, board: List[List[int]]) -> None:
        """
        Do not return anything, modify board in-place instead.
        """
        result = [[col for col in row] for row in board]

        m = len(board) # total row
        n = len(board[0]) # total col

        for row in range(m):
            for col in range(n):
                count = 0

                # row边界值
                if row != 0: # 防止上边界溢出
                    count += board[row - 1][col]
                    if col != n - 1:
                        count += board[row - 1][col + 1]
                    if col != 0:
                        count += board[row - 1][col - 1]

                if row != m - 1: # 防止下边界溢出
                    count += board[row + 1][col]
                    if col != n - 1:
                        count += board[row + 1][col + 1]
                    if col != 0:
                        count += board[row + 1][col - 1]

                # col边界值
                if col != 0: # 防止左边节溢出
                    count += board[row][col - 1]

                if col != n - 1: # 防止有边界溢出
                    count += board[row][col + 1]

                # 处理状态更新
                if board[row][col] == 0 and count == 3:
                    # 本来是0，需要正好3
                    result[row][col] = 1
                elif board[row][col] == 1 and (count < 2 or count > 3):
                    # 本来是1，需要正好2或者3才可以保留
                    result[row][col] = 0
        board[:] = result[:]

复杂度

• 时间：我们先创建了一个复制board全部内容的矩阵result，需要消耗$O(n \cdot m)$。然后循环遍历整个board矩阵，消耗时间也是$O(n \cdot m)$。在遍历结束后还需要把result的值更新回board里面去，同样也是$O(n \cdot m)$的时间，总计就是$O(n \cdot m)$。
• 空间：除了本来就有的board，我们还额外设置了result矩阵，空间消耗为$O(n \cdot m)$，总额外空间消耗就是$O(n \cdot m)$，非空间的最优解。

方法2:

思路

我们既然想要节省空间，就需要按照题目follow up里的要求进行in place的更新，但我们的更新又不能够影响到本来已有的值，因为我们还需要在后续的判断中用到这些值。那逻辑就是不要用1和0在原位更新，创建2和-1或者其他临时更新的数，然后进行更新即可。基于之前的代码进行一下逻辑的实现。

代码

class Solution:
    def gameOfLife(self, board: List[List[int]]) -> None:
        """
        Do not return anything, modify board in-place instead.
        """
        m = len(board) # total row
        n = len(board[0]) # total col

        for row in range(m):
            for col in range(n):
                count = 0

                # row边界值
                if row != 0: # 防止上边界溢出
                    if abs(board[row - 1][col]) == 1:
                        count += 1
                    if col != n - 1:
                        if abs(board[row - 1][col + 1]) == 1:
                            count += 1
                    if col != 0:
                        if abs(board[row - 1][col - 1]) == 1:
                            count += 1

                if row != m - 1: # 防止下边界溢出
                    count += board[row + 1][col]
                    if col != n - 1:
                        count += board[row + 1][col + 1]
                    if col != 0:
                        count += board[row + 1][col - 1]

                # col边界值
                if col != 0: # 防止左边节溢出
                    if abs(board[row][col - 1]) == 1:
                        count += 1

                if col != n - 1: # 防止有边界溢出
                    count += board[row][col + 1]

                # 处理状态更新
                if board[row][col] == 0 and count == 3:
                    # 本来是0，需要正好3
                    # 临时更新为2即可
                    board[row][col] = 2
                elif board[row][col] == 1 and (count < 2 or count > 3):
                    # 本来是1，需要正好2或者3才可以保留
                    # 临时更新 -1（通过abs值不变）
                    board[row][col] = -1

        for row in range(m):
            for col in range(n):
                if board[row][col] == -1:
                    board[row][col] = 0
                elif board[row][col] == 2:
                    board[row][col] = 1

复杂度

• 时间：是没有变化的，虽然少了创建result的时间，但是总时间还是$O(n \cdot m)$。
• 空间：那当然是大大优化的了，完全没有创建额外的矩阵去进行储存，空间消耗就是$O(1)$。

方法3:

思路

前面的代码非常不优雅（全然エレガントじゃない），那我们就调整一下，通过相对坐标的方式对8个方向进行循环更新，其他逻辑不变，也就是如下。

代码

class Solution:
    def gameOfLife(self, board: List[List[int]]) -> None:
        """
        Do not return anything, modify board in-place instead.
        """
        m = len(board)  # total row
        n = len(board[0])  # total col

        for row in range(m):
            for col in range(n):
                count = 0

                # 定义临近细胞的相对坐标
                neighbors = [
                    (-1, -1), (-1, 0), (-1, 1),
                    (0, -1),         (0, 1),
                    (1, -1), (1, 0), (1, 1)
                ]

                # 统计活细胞数量
                for dr, dc in neighbors:
                    # 使用相对偏移两更新row和col
                    r = row + dr
                    c = col + dc
                    if 0 <= r < m and 0 <= c < n: # 防止超界
                        # 只统计当前活细胞（绝对值为 1）
                        if abs(board[r][c]) == 1:
                            count += 1

                # 处理状态更新
                if board[row][col] == 0 and count == 3:
                    # 当前为 0，且有正好 3 个活细胞时变1
                    board[row][col] = 2
                elif board[row][col] == 1 and (count < 2 or count > 3):
                    # 当前为 1，且邻居活细胞少于 2 或多于 3 时变0
                    board[row][col] = -1

        # 第二次遍历，恢复最终状态
        for row in range(m):
            for col in range(n):
                if board[row][col] == -1:
                    board[row][col] = 0
                elif board[row][col] == 2:
                    board[row][col] = 1

复杂度

• 与前一个方法2的时间与空间复杂度是完全一样的。